WP3-24: Difference between revisions
| (4 intermediate revisions by one other user not shown) | |||
| Line 18: | Line 18: | ||
|- | |- | ||
| TRL || 3-4 | | TRL || 3-4 | ||
|- | |||
| Contact || mario.diferdinando at univaq.it | |||
|} | |} | ||
| Line 59: | Line 61: | ||
==Contribution and Improvements== | ==Contribution and Improvements== | ||
The pipelined implementation technique, here proposed in the context of UAVs control (WP3-24), allows lower execution times, and hence smaller sampling times, than its naive implementation. Moreover, the power consumption of the pipelined control algorithm is lower. These two aspects constitute the main benefits of using a pipelining technique for the implementation of UAV control algorithm on an FPGA. In other words, the main aim behind the component (WP3-24) is to provide an implementation guideline for UAVs control algorithms showing that, when technological solutions such as FPGAs are used, the pipelining methodology can be successfully applied to obtain lower sampling periods, thereby allowing the implementation of more sophisticated controllers for UAVs. The efficiency of the proposed implementation methodology is shown by developing on FPGA a robust sampled—data controller for the autonomous navigation of drone which has been designed in the context of WP4 for C4D project. Finally, through experimental results, it can be shown that the pipelining methodology also allows taking into account the energetic aspects of the controller implementations, and not only the controller performance. This is another very important aspect for onboard systems as in UAVs. | The pipelined implementation technique, here proposed in the context of UAVs control (WP3-24), allows lower execution times, and hence smaller sampling times, than its naive implementation. Moreover, the power consumption of the pipelined control algorithm is lower. These two aspects constitute the main benefits of using a pipelining technique for the implementation of UAV control algorithm on an FPGA. In other words, the main aim behind the component (WP3-24) is to provide an implementation guideline for UAVs control algorithms showing that, when technological solutions such as FPGAs are used, the pipelining methodology can be successfully applied to obtain lower sampling periods, thereby allowing the implementation of more sophisticated controllers for UAVs. The efficiency of the proposed implementation methodology is shown by developing on FPGA a robust sampled—data controller for the autonomous navigation of drone which has been designed in the context of WP4 for C4D project. Finally, through experimental results, it can be shown that the pipelining methodology also allows taking into account the energetic aspects of the controller implementations, and not only the controller performance. This is another very important aspect for onboard systems as in UAVs. | ||
The proposed methodology has been validated through simulations. In particular, the following scenario has been addressed: the drone has to follows a trajectory resembles a complete mission with a duration of several minutes, where the UAV goes through a artichoke with a constant velocity. Such a reference is generated as a b–spline from the given waypoints. | |||
The system has been simulated in different combinations through the implementation steps, the quadrotor model has been always considered as continuous–time (although numerically integrated using multi–step algorithms, ensuring better accuracy and stability than single step integration). In particular, in the considered scenarios, the UAV to be controlled can be selected between different simulators: | |||
• Simulink: implemented through differential equations describing the mathematical model with the main dynamics, it is the fastest in terms of simulation being directly integrated. | |||
• Amesim: implemented as a complex yet detailed model, providing high fidelity dynamics, it is sufficiently fast in simulation despite the detailed model. | |||
• Coppeliasim: implemented as a mixed model, calculating force and torque from the mathematical model equations, but using Coppeliasim’s physics engine, it is slower than the other choices but provides a complete 3D environment along with physical interaction with other objects such as collision. | |||
The controller followed this development flow, each step has an associated brief name and description for reference: | |||
1. Ideal: continuous–time, double–precision floating–point arithmetic, full precision operations, ideal derivative, no internal arithmetic saturation. | |||
2. Discrete: discrete–time, still with double–precision floating–point arithmetic and full precision operations and no saturation, filtered discrete–time derivative. | |||
3. Normalized: discrete–time, full precision arithmetic and operations, normalized inputs, outputs, and internal variables, with internal arithmetic saturation. | |||
4. Fixed–point: discrete–time, normalized fixed–point arithmetic, with full precision operations and internal arithmetic saturation, filtered derivative. | |||
5. Approximated: discrete–time, normalized fixed–point arithmetic, approximated operations, arithmetic saturation, filtered derivative. | |||
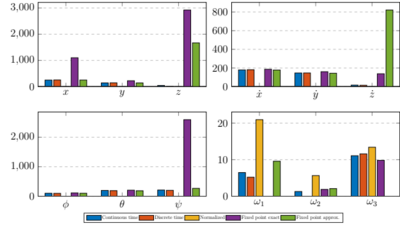
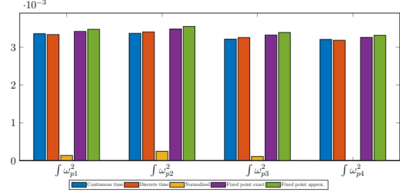
Some simulation results are reported in the figure below. | |||
[[File:Prova03.png|400px|Figure 4. Mean square error.]] | |||
[[File:Prova04.png|400px|Figure 5. Propeller velocity square integral.]] | |||
From the performance indicators charts some conclusions can be pointed out: | |||
• A trend is mostly evident, where almost all of the indicators get progressively better, from the initial continuous–time implementation up to the normalized version, but after the latter the indicators get worse, almost returning to the original performance level: | |||
a. Being the starting point, the continuous–time controller represents the performance reference for subsequent versions. | |||
b. The discrete–time implementation also contains a derivative optimization, leading to a slightly better performance. | |||
c. The normalized version adds more improvements due to a better use of the available (double–precision floating–point) arithmetic and an accurate management of critical calculations, in fact it presents the best overall performance according to the indicators. | |||
d. The introduction of fixed–point arithmetic introduces intrinsic approximations, worsening the performance gained in the previous version. | |||
e. Finally substituting several operations with look–up tables introduce more approximations, taking back the improvements to the starting point. | |||
• The objective of this work has been reached since the final overall performance is comparable to the original version while the final one has several advantages: | |||
f. It provides a fully synthesizable code enabling FPGA implementation or even specialized ASIC manufacturing. | |||
g. It results in an area/resource efficient system, allowing independent usage alongside another processing system, freeing the latter from the control task. | |||
h. Lower complexity brings also lower power consumption, although marginal when considering the overall consumption. | |||
==References== | |||
[1] C. Acosta Lua, C.C. Vaca Garcia, S. Di Gennaro, B. Castillo--Toledo, and M.E. Sanchez Morales, Real--Time Hovering Control of Unmanned Aerial Vehicles, Mathematical Problems in Engineering, Vol. 2020, pp. 1--8, 2020. | |||
[2] J.T. Guillen--Bonilla, C.C. Vaca Garcia, S. Di Gennaro, M.E. Sanchez Morales, C. Acosta Lua, Vision--Based Nonlinear Control of Quadrotors Using the Photogrammetric Technique, Mathematical Problems in Engineering, Vol. 2020, pp. 1--10, 2020. ISSN: 1024-12. | |||
[3] C. A. Lúa, S. D. Gennaro et. al., Digital Implementation via FPGA of Controllers for Active Control of Ground Vehicles, IEEE Trans. on Ind. Inf., vol 15, pp 2253-2264, 2019. | |||
Latest revision as of 08:40, 10 March 2023
Efficient digital implementation of controllers on FPGAs
| ID | WP3-24 |
| Contributor | UNIVAQ |
| Levels | Methodological |
| Require | FPGAs for the implementation of the proposed control algorithms |
| Provide | An efficient methodology for the implementation of digital control algorithms on FPGAs based on the pipeline approach. |
| Input | Control algorithms for the autonomous navigation of drones to be implemented on FPGAs |
| Output | Lower execution times, and hence smaller sampling times, than its naive implementation. Lower power consumption of the pipelined control algorithm. |
| C4D building block | Flight Control. |
| TRL | 3-4 |
| Contact | mario.diferdinando at univaq.it |
Detailed Description
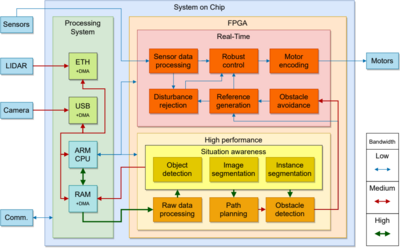
Efficient digital implementation of controllers on FPGAs. In the context of C4D project, the component WP3-24 aims to provide an efficient methodology for the digital implementation of controllers on FPGAs. It is well-known that the use of UAVs in many complex tasks has increased the complexity of the embedded control algorithms that are necessary in order to face more challenging performances, such as: detection and avoiding of obstacles; cooperation among drones; efficient trajectory execution; etc. However, many software solutions also present some limitations, due to its fixed internal architecture. This leads to a full serialization of the data treatment. The more complex is the control and decision algorithm, the longer is its execution time. This, in turn, constitutes a lower bound for the sampling time that can be used in the specific application. Clearly, longer sampling times determine worse controller performances. To obtain higher control performances, one can work in two possible directions. The first is methodological, and consists of designing the control algorithms on the basis of better discrete-time dynamic representations of the vehicle. The second is technological, and regards the use of more performing devices used to implement a given controller. As far as the technological solution is concerned, field-programmable gate arrays (FPGAs) can ensure better performances than software solutions, thanks to the possibility of parallelism and to the increasing integration density, which allows implementing complex control algorithms. In fact, FPGAs are full system-on-chip (SoC) solutions. They allow more flexibility for the implementation of embedded controllers, due to the fact that they include in the same chip various components (processors, memories, hardware multiplier blocks, analog–digital converters, matrix of programmable logic elements-fabric-and buses). The fact that FPGAs integrate both software and hardware resources allow faster implementations of controllers making use of the parallelism. Therefore, FPGAs constitute a valid hardware solution, since it is possible to design an architecture that is customized for the control algorithm to be implemented. This ensures shorter execution times of the algorithm. To further reduce the execution time in FPGAs, some techniques can be used that allow transforming the circuit structure, in order to reduce this time, and possibly the power consumption, maintaining the desired functionality, i.e., implementing the required control input. These (methodological, not technological) techniques include retiming/pipelining, folding/unfolding, interleaving, etc. The proposed methodology for the efficient implementation of controllers on FPGA is focused on retiming and pipelining. The former is a transformation technique used to change the locations of the delay elements in a circuit without affecting the input/output characteristics of the circuit. Pipelining is a special case of retiming used to reduce the critical path, introducing pipelining latches along the data path. Shortening the critical paths, one can increase the clock speed or the sample speed, or one can reduce the power consumption at the same speed.
In order to be functional, the resulting controller must respect certain constraints given by the specific application, in this case:
• Real–time execution represents a hard constraint, meaning that exceeding the allowed time for the control action calculation is unacceptable.
• Power consumption is significant because the final controller will be powered from the UAV’s battery.
• Size and weight are directly related to power consumption, but also to manoeuvrability if they are too high.
• Precision can be traded for better performances and power efficiency if kept inside acceptable bounds.
• Reliability must be always ensured, although different implementations can provide several ways to obtain it.
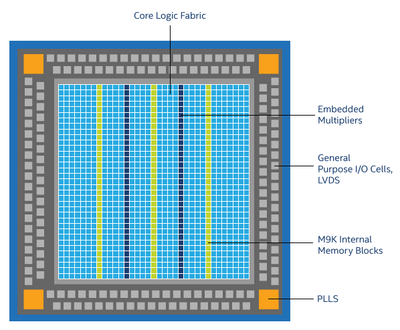
A perfect candidate for this application is the FPGA implementation, since it can provide strict real–time execution, high power efficiency, small size, and high reliability, at the cost of a reduced dynamic range. For instance, the Intel Cyclone 10 LP FPGA was available and corresponded to what was needed, then it has been used as a reference, it comes on a minimal board, useful for actual power consumption tests and fast prototyping, allowing installation on small UAVs for real world tests (see the figure below)
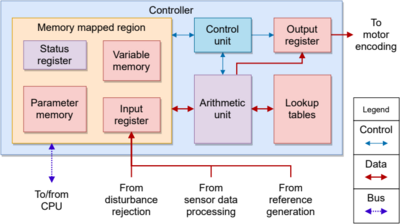
Depending on the final implementation strategy, the resulting architecture could be an application specific processor, with the sole purpose of managing the calculations autonomously, in other words it could result in a finite state machine managing a small arithmetic unit. This would ensure minimal area usage and maximum efficiency, yet fully respecting the timing constraints as this kind of processor will have only one task at any time:
1. Receive estimated state and reference input data.
2. Perform calculations in a fixed, appropriate allowed time frame, as a sequence of internal operations opaque to the external interface.
3. Provide control outputs to the actuators.
4. Wait to start a new cycle (if, as desired, the calculation takes less than the allowed time frame, in other words it should have minimal input–output delay).
Other advantages of such architecture are reliability, since the entire cycle is well known in advance and the processor has no unexpected behaviors, unless there are environmental factors outside of the designer’s control, in those cases redundancy schemes can be applied, even on the same FPGA: duplicating or triplicating the same design and determining the correct output by voting, a high level of reliability can be ensured, since the stabilization control of the UAV is a critical task. Taking up very few hardware resources, the rest of the device can be used for other purposes, such as sensor data elaboration, mission planning (through a general purpose soft–processor), path planning, image elaboration, obstacle detection and avoidance, which greatly benefit from a hardware implementation. Another possible approach, yet to be explored, to improve reliability is the use of parity bits to detect errors, in fact FPGAs almost always make use of memory blocks and embedded multiply–accumulate blocks with the required bit widths, the one considered here indeed provides 9 bits per word native memory (can be used in several different configurations, such as 18 or 16 bits per word) and 18 bits in – 36 bits out multipliers (can be also used as two separate, independent 9 bits in – 18 bits out multipliers). If the word is considered as a multiple of one byte, with 8 bits per byte, then one parity bit is available since the native word is 9 bits wide. Native bit widths are especially important and need to be kept in mind for a maximally efficient implementation. Single event upset at configuration time is now fully supported by several vendors. One more thing worth mentioning, made possible by FPGAs, is the update process while the controller is still functioning: having redundant units allows an in–place reconfiguration of one of them while the others ensure functionality, through partial reconfiguration. From the control point of view, this architecture choice allows to implement a supervisor to be used along with the controller, this supervisor could be a disturbance estimator, to correct and react to external unknown events (see the figures below).
Contribution and Improvements
The pipelined implementation technique, here proposed in the context of UAVs control (WP3-24), allows lower execution times, and hence smaller sampling times, than its naive implementation. Moreover, the power consumption of the pipelined control algorithm is lower. These two aspects constitute the main benefits of using a pipelining technique for the implementation of UAV control algorithm on an FPGA. In other words, the main aim behind the component (WP3-24) is to provide an implementation guideline for UAVs control algorithms showing that, when technological solutions such as FPGAs are used, the pipelining methodology can be successfully applied to obtain lower sampling periods, thereby allowing the implementation of more sophisticated controllers for UAVs. The efficiency of the proposed implementation methodology is shown by developing on FPGA a robust sampled—data controller for the autonomous navigation of drone which has been designed in the context of WP4 for C4D project. Finally, through experimental results, it can be shown that the pipelining methodology also allows taking into account the energetic aspects of the controller implementations, and not only the controller performance. This is another very important aspect for onboard systems as in UAVs.
The proposed methodology has been validated through simulations. In particular, the following scenario has been addressed: the drone has to follows a trajectory resembles a complete mission with a duration of several minutes, where the UAV goes through a artichoke with a constant velocity. Such a reference is generated as a b–spline from the given waypoints.
The system has been simulated in different combinations through the implementation steps, the quadrotor model has been always considered as continuous–time (although numerically integrated using multi–step algorithms, ensuring better accuracy and stability than single step integration). In particular, in the considered scenarios, the UAV to be controlled can be selected between different simulators:
• Simulink: implemented through differential equations describing the mathematical model with the main dynamics, it is the fastest in terms of simulation being directly integrated.
• Amesim: implemented as a complex yet detailed model, providing high fidelity dynamics, it is sufficiently fast in simulation despite the detailed model.
• Coppeliasim: implemented as a mixed model, calculating force and torque from the mathematical model equations, but using Coppeliasim’s physics engine, it is slower than the other choices but provides a complete 3D environment along with physical interaction with other objects such as collision.
The controller followed this development flow, each step has an associated brief name and description for reference:
1. Ideal: continuous–time, double–precision floating–point arithmetic, full precision operations, ideal derivative, no internal arithmetic saturation.
2. Discrete: discrete–time, still with double–precision floating–point arithmetic and full precision operations and no saturation, filtered discrete–time derivative.
3. Normalized: discrete–time, full precision arithmetic and operations, normalized inputs, outputs, and internal variables, with internal arithmetic saturation.
4. Fixed–point: discrete–time, normalized fixed–point arithmetic, with full precision operations and internal arithmetic saturation, filtered derivative.
5. Approximated: discrete–time, normalized fixed–point arithmetic, approximated operations, arithmetic saturation, filtered derivative.
Some simulation results are reported in the figure below.
From the performance indicators charts some conclusions can be pointed out:
• A trend is mostly evident, where almost all of the indicators get progressively better, from the initial continuous–time implementation up to the normalized version, but after the latter the indicators get worse, almost returning to the original performance level:
a. Being the starting point, the continuous–time controller represents the performance reference for subsequent versions.
b. The discrete–time implementation also contains a derivative optimization, leading to a slightly better performance.
c. The normalized version adds more improvements due to a better use of the available (double–precision floating–point) arithmetic and an accurate management of critical calculations, in fact it presents the best overall performance according to the indicators.
d. The introduction of fixed–point arithmetic introduces intrinsic approximations, worsening the performance gained in the previous version.
e. Finally substituting several operations with look–up tables introduce more approximations, taking back the improvements to the starting point.
• The objective of this work has been reached since the final overall performance is comparable to the original version while the final one has several advantages:
f. It provides a fully synthesizable code enabling FPGA implementation or even specialized ASIC manufacturing.
g. It results in an area/resource efficient system, allowing independent usage alongside another processing system, freeing the latter from the control task.
h. Lower complexity brings also lower power consumption, although marginal when considering the overall consumption.
References
[1] C. Acosta Lua, C.C. Vaca Garcia, S. Di Gennaro, B. Castillo--Toledo, and M.E. Sanchez Morales, Real--Time Hovering Control of Unmanned Aerial Vehicles, Mathematical Problems in Engineering, Vol. 2020, pp. 1--8, 2020.
[2] J.T. Guillen--Bonilla, C.C. Vaca Garcia, S. Di Gennaro, M.E. Sanchez Morales, C. Acosta Lua, Vision--Based Nonlinear Control of Quadrotors Using the Photogrammetric Technique, Mathematical Problems in Engineering, Vol. 2020, pp. 1--10, 2020. ISSN: 1024-12.
[3] C. A. Lúa, S. D. Gennaro et. al., Digital Implementation via FPGA of Controllers for Active Control of Ground Vehicles, IEEE Trans. on Ind. Inf., vol 15, pp 2253-2264, 2019.