WP4-33: Difference between revisions
| Line 36: | Line 36: | ||
Simulations of the provided control algorithm have been performed. A comparison of the robustified controller with the non-robustified one is also carried out. See figures 1-4. | Simulations of the provided control algorithm have been performed. A comparison of the robustified controller with the non-robustified one is also carried out. See figures 1-4. | ||
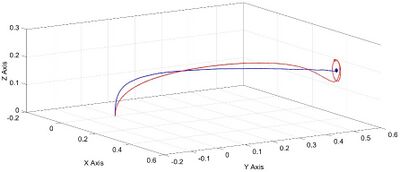
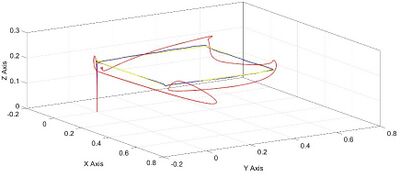
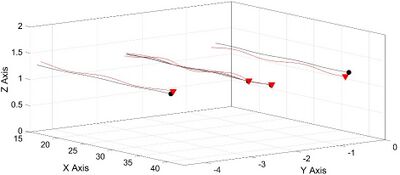
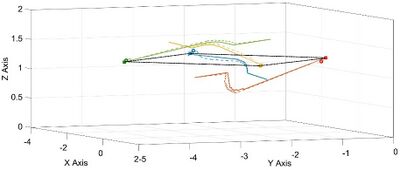
[[File:01.jpg|400px|Figure 1. Trajectory of the quadcopter along x, y and z axes: the desired position in the space is reported with a rhomboidal black point; the trajectory of the quadcopter in the case of robustified and non robustified controller is reported in blue and red line, respectively.]] | [[File:01.jpg|400px|Figure 1. Trajectory of the quadcopter along x, y and z axes: the desired position in the space is reported with a rhomboidal black point; the trajectory of the quadcopter in the case of robustified and non robustified controller is reported in blue and red line, respectively.]] [[File:02.jpg|400px|Figure 2 Trajectory of the quadcopter along x, y and z axes: the desired trajectory in the space is reported with a yellow line; the trajectory of the quadcopter in the case of robustified and non robustified controller is reported in blue and red line, respectively.]] | ||
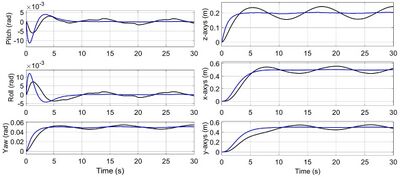
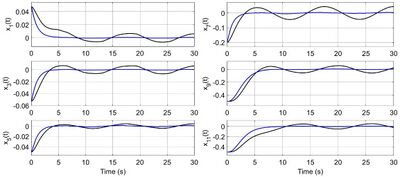
[[File:03.jpg|400px|Figure 3. Angles and positions of the UAV: the trajectory of the quadcopter in the case of robustified and non robustified controller is reported in blue and black line, respectively.]] [[File:04.jpg|400px|Figure 4. Tracking errors for angles and position of the UAV: the trajectories of the tracking errors in the case of robustified and non robustified controller are reported in blue and black lines, respectively.]] | |||
[[File:03.jpg|400px|Figure 3. Angles and positions of the UAV: the trajectory of the quadcopter in the case of robustified and non robustified controller is reported in blue and black line, respectively.]] | |||
[[File:04.jpg|400px|Figure 4. Tracking errors for angles and position of the UAV: the trajectories of the tracking errors in the case of robustified and non robustified controller are reported in blue and black lines, respectively.]] | |||
Controlling Swarms of Drones | Controlling Swarms of Drones | ||
Revision as of 10:08, 3 April 2022
Autonomy, cooperation, and awareness
| ID | WP4-33 |
| Contributor | UNIVAQ |
| Levels | Methodological |
| Require | Sensors, actuators and computing devices. |
| Provide | An efficient methodology for the design of robust digital control algorithms for the autonomous and cooperative navigation of UAVs. |
| Input | Measurements from sensors signal. |
| Output | Control actions. |
| C4D building block | Flight Control. |
| TRL | 3-4 |
Detailed Description
One of the main challenges when dealing with drone flight control systems is to provide control algorithms taking into account possible measurement errors as well as possible actuation disturbances. Indeed, in practical operative situations, the measurements provided by the sensors to the drone flight control are often affected by errors mainly due to devices uncertainties. As well, the actuators involved in the control actions (i.e., the drone motors) are often affected by disturbances due to possible malfunctioning of the motors or to uncertainties in the devices which make use of the control input. In the literature concerning drone flight control systems, control algorithms are often provided without taking into account of such possible issues. Moreover, such control algorithms are often designed in a continuous-time basis and problems concerning the sampling and the quantization of the control law are not taken into account. These facts easily lead to a deterioration of the performances when such control algorithms are applied in practice. The drone flight control should be able to compensate and reject possible actuation disturbances and measurement uncertainties. Furthermore, the control algorithm should be designed by taking into account the sampling and the quantization of the input/output channels. In the context of UC 5, the developed software concerns a novel robust sampled—data control strategy allowing the attenuation of bounded actuation disturbances as well as of bounded observation error.
It is well-known that a swarm of drone, in which each agent locally interacts with the other agents and the environment, is able to perform complex tasks which are not achievable by the use of a single agent. Therefore, the use of multiple UAVs as an organized swarm can significantly increase the performances of the single UAV, as well as of the overall group (see [1]-[3]). Indeed, each agent of the swarm is allowed to make use of the resources and capabilities of other agents through communication and/or coordination, and provide it with extra capabilities. Many approaches to the formation control problem of UAVs have been presented in the literature (see, among the others, [4]-[9]). On the other hand, contributions which simultaneously address time-varying formation, switching topology and the collision avoidance have never been provided. In the context of UCs 4 and 5, the developed software concerns a novel control strategy for the deployment of multi-UAV systems in a distributed time-varying set-up, where UAVs rely on local communication and computation. In particular, the control algorithm allows the main swarm intelligence strategies, namely flight formation, swarm tracking, and social foraging. Finally, the robust control strategy proposed in Section 1.1 is integrated to the algorithm and an efficient methodology for its implementation on FPGAs is presented.
Contribution and Improvements
Robust Digital Control for Autonomous Navigation
In the context of UC 5, in order to provide a control strategy for the compensation and rejection of environmental perturbations, measurement uncertainties, and possible faults, a robustified quantized sampled-data drone flight controller is proposed. In particular, by the use of ISS (Input-to-State Stability) redesign methodology (see, for instance, [13]), a new term to be added to the feedback is designed in order to make it robust with respect to any bounded measurement error as well as any bounded actuation disturbance. Then, the stabilization in the sampled-and-hold sense theory (see [10]-[12]) is used as tool for analytically proving the existence of a suitably small sampling period and of an accurate quantization of the input/output channels such that the semi-global practical stability of the related quantized sampled-data closed-loop system with arbitrarily small final tracking error is ensured. It is highlighted that such control algorithm does not need any knowledge concerning the nature of the measurement errors and of the actuation disturbances. The only knowledges required for the implementation of the control algorithm are their amplitude bounds. Moreover, the provided algorithm is a static state feedback controller which can be easily implemented on FPGAs. Summarizing, in the context of UC5, the provided control algorithm contributes to the following requirements: • managing of critical situation with improved situation awareness (task interferences, scheduling issues, fault of failure conditions) • providing efficient digital implementation of discrete–time controllers on FPGAs • compensate and reject environmental perturbations, and measurement uncertainties. Simulations of the provided control algorithm have been performed. A comparison of the robustified controller with the non-robustified one is also carried out. See figures 1-4.
Controlling Swarms of Drones
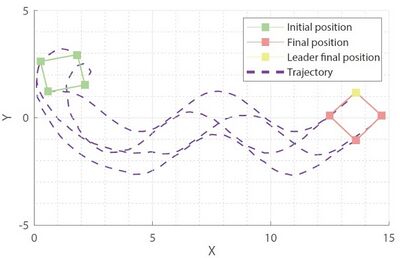
The proposed component concerns a distributed control strategy for swarms of drones based on the leader-follower consensus approach which allow to take into account time-varying formations and switching topologies, while ensuring the collision avoidance of multi-UAVs and the rejection of environmental perturbations, and measurement uncertainties. The software is based on a distributed control strategy for steering the agents of the swarm towards a collection point. In order to cope with the formation control, a procedure to arrange agents in a family of geometric formations is included in the software. Swarm tracking is allowed by including also a distributed mechanism based on the so-called leader-following consensus to move the entire swarm in accordance with a predefined trajectory. Moreover, a social foraging strategy that allows agents to avoid obstacles is included in the software by imposing on-line a time-varying formation pattern. Finally, a software component for the attenuation of actuation disturbances and measurements errors is developed and integrated to the control strategy (see forthcoming Section 4). The provided algorithm can be easily implemented on FPGAs. An efficient methodology for the implementation of the provided component will be also presented (see forthcoming Section 4). Summarizing, the developed software simultaneously addresses a challenging time-varying distributed set-up of the UAVs, characterized by the following features: (i) each UAV has limited resources in terms of communication coverage, so that it can only receive information locally from a time-varying subset of the swarm; (ii) the UAVs are required to dynamically avoid obstacles by imposing on-line a time-varying formation pattern; (iii) both the topology of communication and the configuration of leader and followers are time-varying. Summarizing, in the context of UC5, the provided control algorithm contributes to the following requirements: • autonomous and cooperative flight of UAVs • managing of critical situation with improved situation awareness (obstacle avoidance, constrained communication) • providing efficient digital implementation of discrete–time controllers on FPGAs • compensate and reject environmental perturbations, and measurement uncertainties. In Figs. 5-8, simulations of the proposed control algorithm are reported.
References
[1] A. Bandala, E. Dadios, R. Vicerra, L. G. Lim, “Swarming algorithm for unmanned aerial vehicle (UAV) quadrotors: Swarm behavior for aggregation, foraging, formation, and tracking”, J. Adv. Comput. Intell. Intell. Inform., vol. 18, 2014, pp 745-751.
[2] A. Kushleyev, D. Mellinger, C. Powers, V. Kumar, “Towards a swarm of agile micro quadrotors”, Auton. Robots, vol. 35, 2013, pp 287-300.
[3] C. Wang, H. Tnunay, Z. Zuo, B. Lennox, Z. Ding, “Fixed-time formation control of multirobot systems: Design and experiments”, IEEE Trans. Ind. Electron., vol. 66, 2019, pp 6292-6301.
[4] Z. Song, C. Duan, J. Wang, Q. Wu, “Chattering-free full-order recursive sliding mode control for finite-time attitude synchronization of rigid spacecraft”, J. Franklin Inst., vol. 356, 2019, pp 998-1020.
[5] J. Wang, Z. Zhou, C. Wang, J. Shan, “Multiple quadrotors formation flying control design and experimental verification”, Unmanned Syst., vol. 7, 2019, pp 47-54.
[6] Z. Gu, P. Shi, D. Yue, Z. Ding, “Decentralized adaptive event-triggered h_∞ filtering for a class of networked nonlinear interconnected systems”, IEEE Trans. Cybern., vol. 49, 2018, pp 1570-1579.
[7] B. Mu, Y. Shi, “Distributed LQR consensus control for heterogeneous multiagent systems: Theory and experiments”, IEEE/ASME Trans. Mech., vol. 23, 2018, pp 434-443.
[8] S. Zhao, “Affine formation maneuver control of multi-agent systems”, IEEE Trans. Autom. Contr., vol. 63, 2018, pp 4140-4155.
[9] S. Zhao, D. Dimarogonas, Z. Sun, D. Bauso, “A general approach to coordination control of mobile agents with motion constraints”, IEEE Trans. Automat. Contr., vol. 63, 2018, pp 1509-1516.
[10] F. H. Clarke, “Discontinuous feedback and nonlinear systems”, Plenary Lecture at IFAC Conference on Nonlinear Control Systems, 2010.
[11] F. H. Clarke, Y. S. Ledyaev, E. D. Sontag and A. I. Subbotin, “Asymptotic controllability implies feedback stabilization”, IEEE Trans. Automat. Control, vol. 42, 1997, pp 1394-1407.
[12] P. Pepe, ”Robustification of nonlinear stabilizers in the sample-and-hold sense”, Journal of The Franklin Institute, vol. 42, 2015, pp 4107-4128.
[13] E. D. Sontag, “Smooth stabilization implies coprime factorization”, IEEE Trans. Automat. Control, vol. 34, 1989, pp 435-443.